
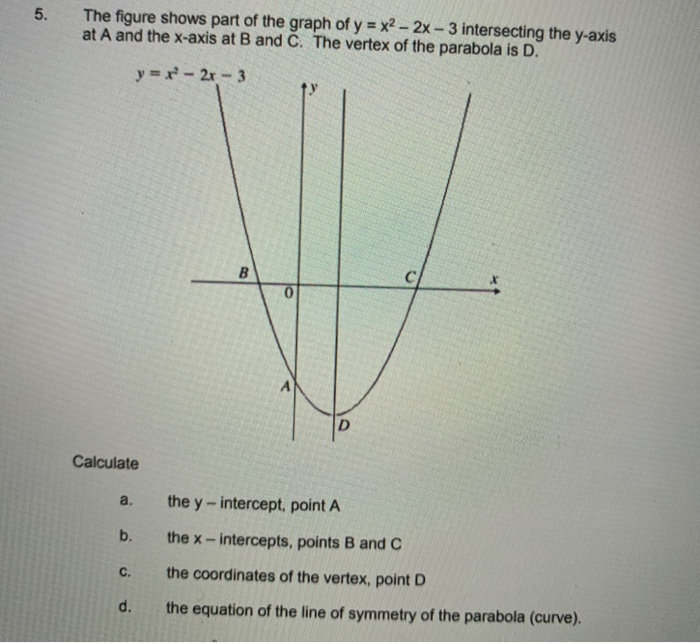
Parabolas Xcelerate Math
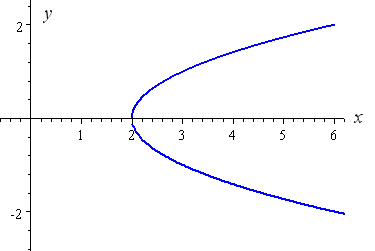
This is what I have so far (I'm mostly stuck on the integration part) $${dy\over dx}=2x \Rightarrow L=\int_0^1 \sqrt{1(2x)^2}dx$$ Substit Stack Exchange Network Stack Exchange network consists of 179 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, andAnd y = −√ x (the bottom half of the parabola) Here is the curve y 2 = x It passes through (0, 0) and also (4,2) and (4,−2) Notice that we get 2 values of y for each value of x larger than 0 This is not a function, it is called a relation
Y=(x-3)^2 parabola
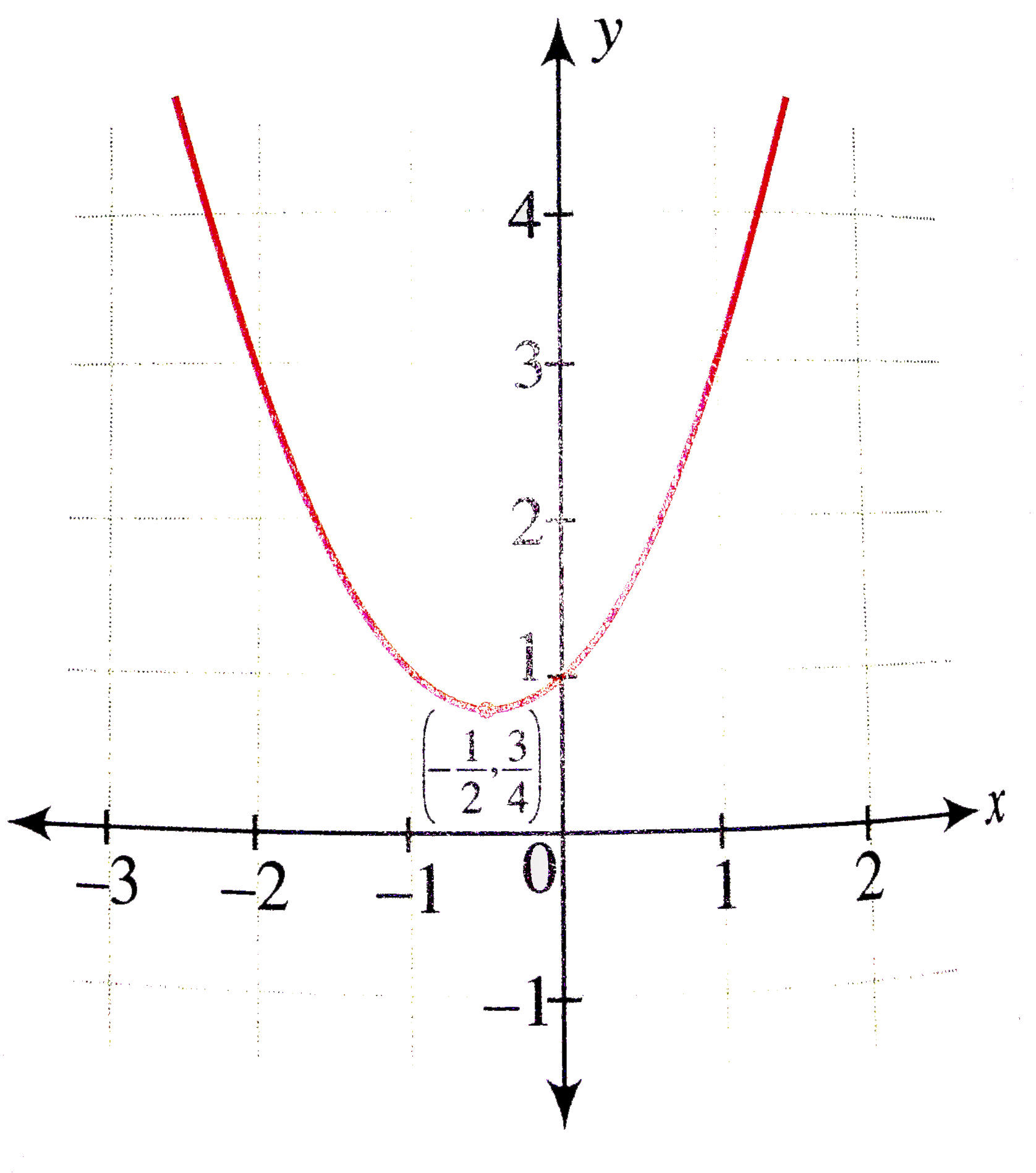
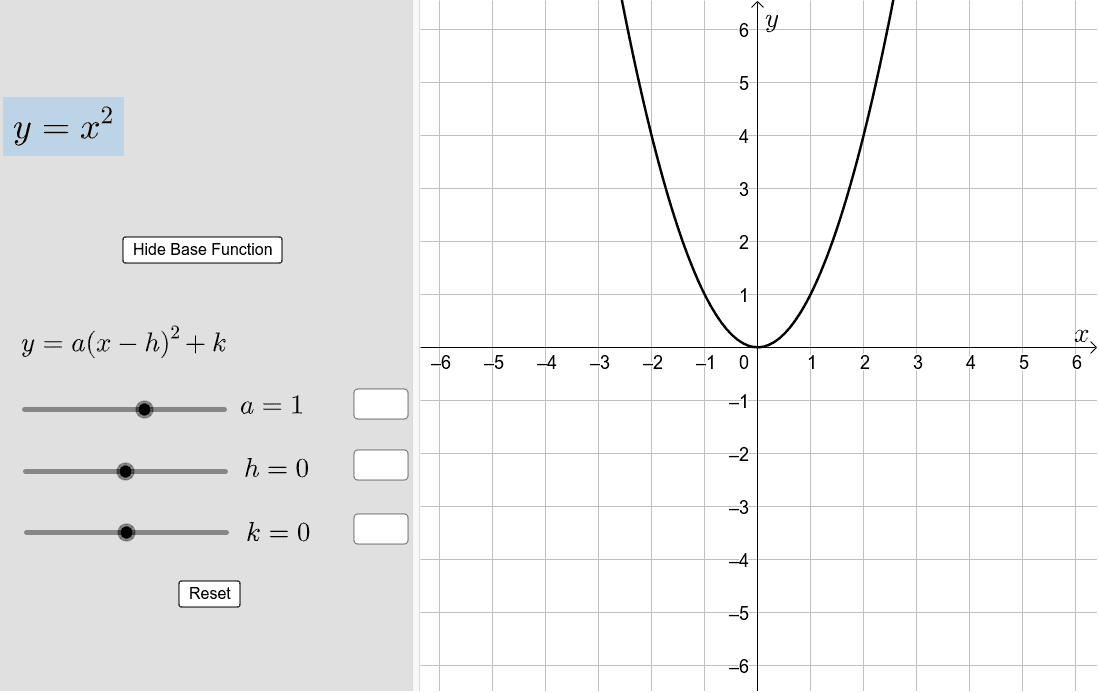
Y=(x-3)^2 parabola-Graphing y = (x h) 2 k In the graph of y = x 2, the point (0, 0) is called the vertex The vertex is the minimum point in a parabola that opens upward In a parabola that opens downward, the vertex is the maximum point We can graph a parabola with aThe general equation of a parabola is y = a(xh) 2 k or x = a(yk) 2 h, where (h,k) denotes the vertex The standard equation of a regular parabola is y 2 = 4ax Some of the important terms below are helpful to understand the features and parts of a parabola Focus The point (a, 0) is the focus of the parabola
Content Transformations Of The Parabola
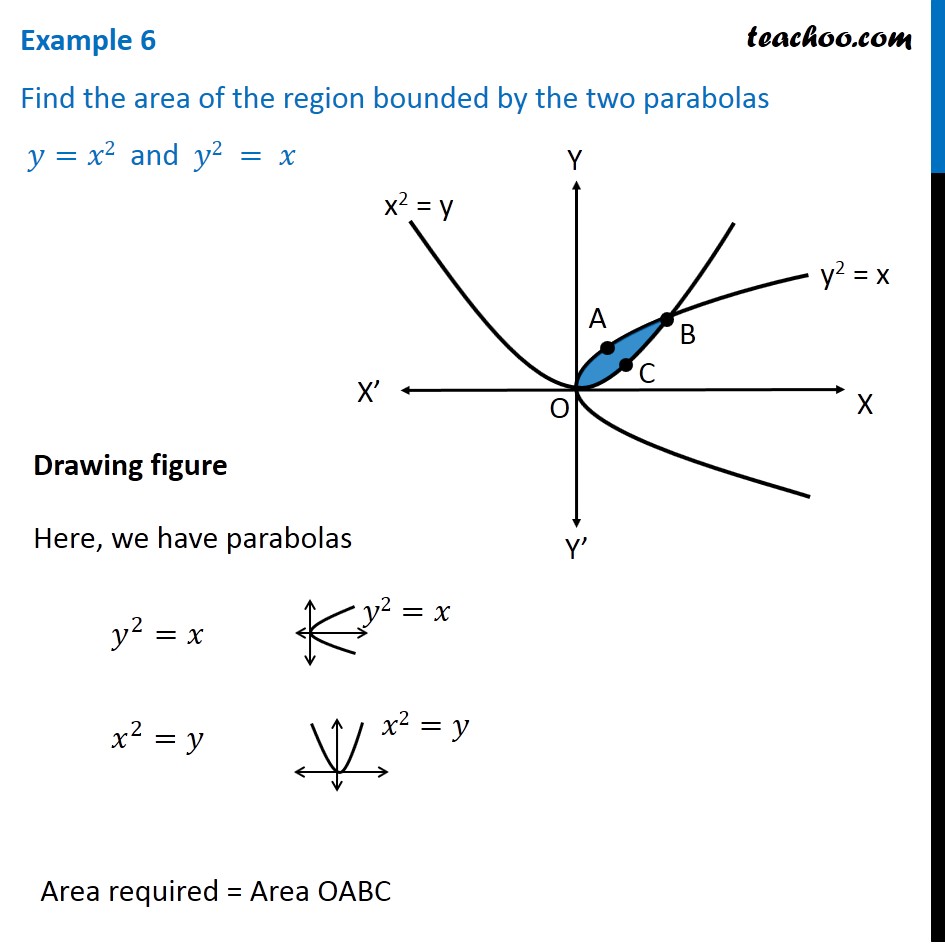
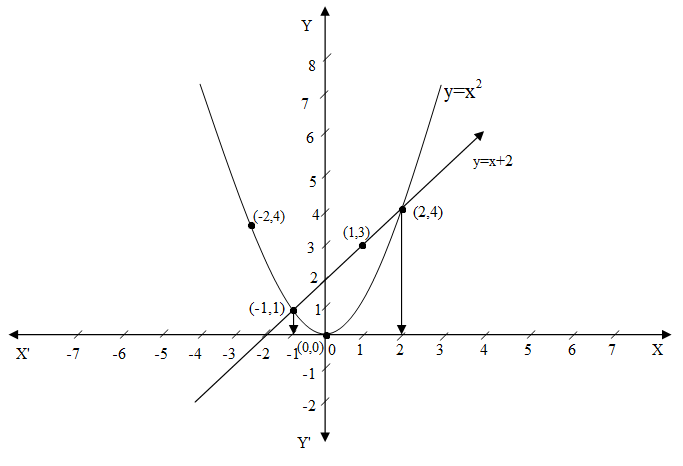
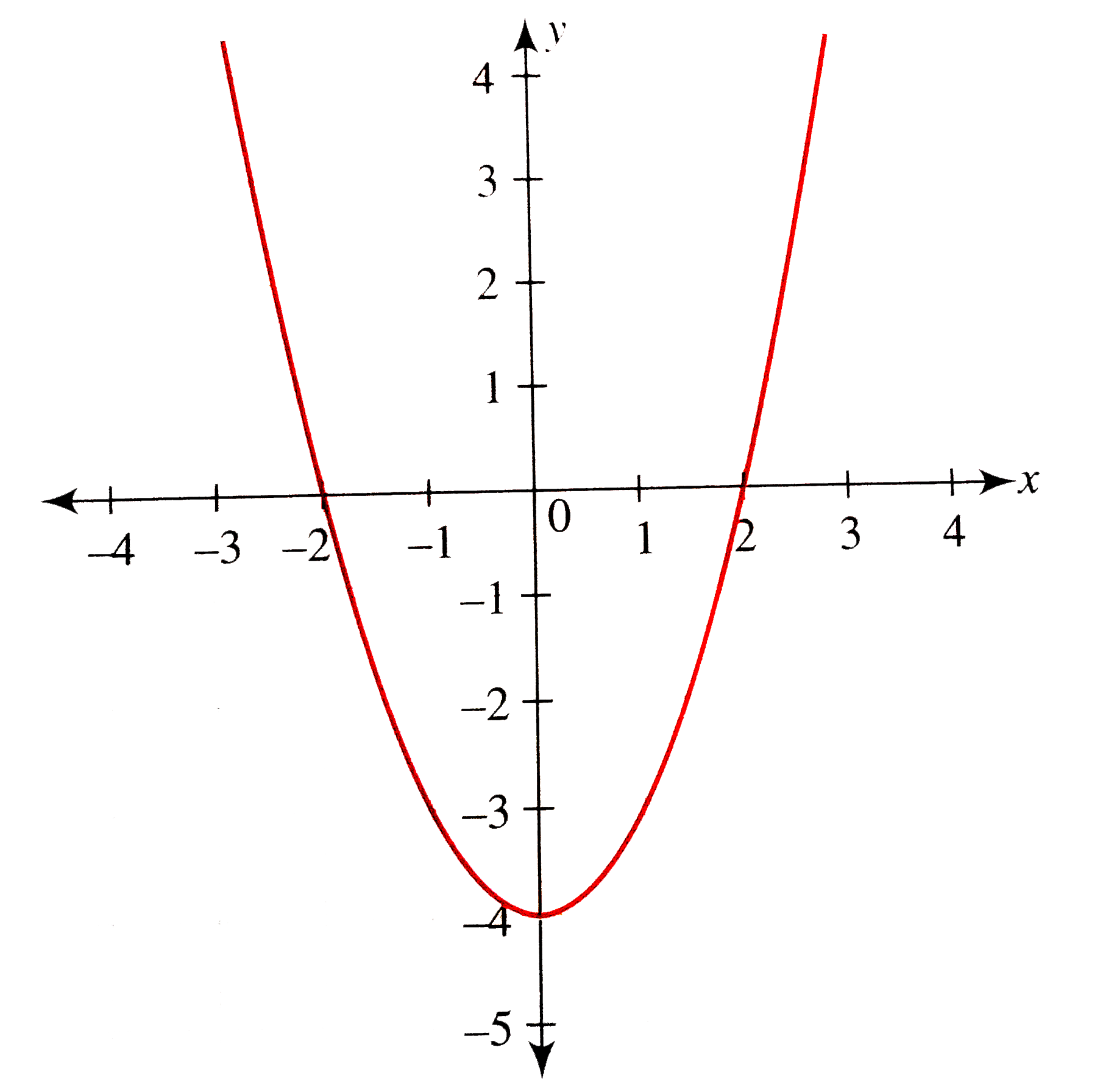
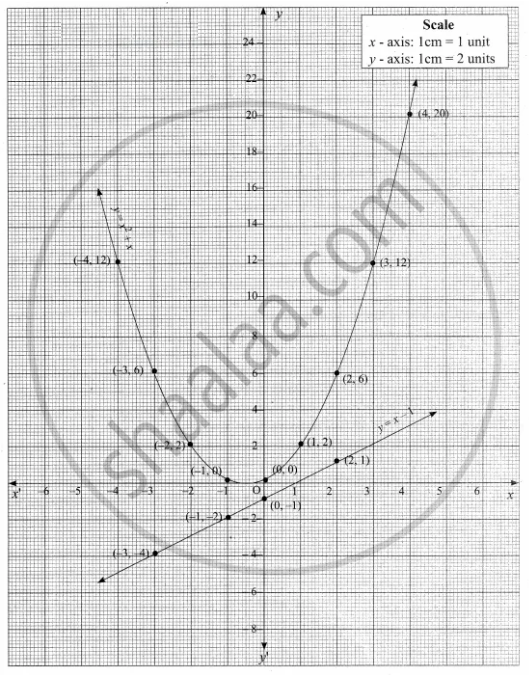
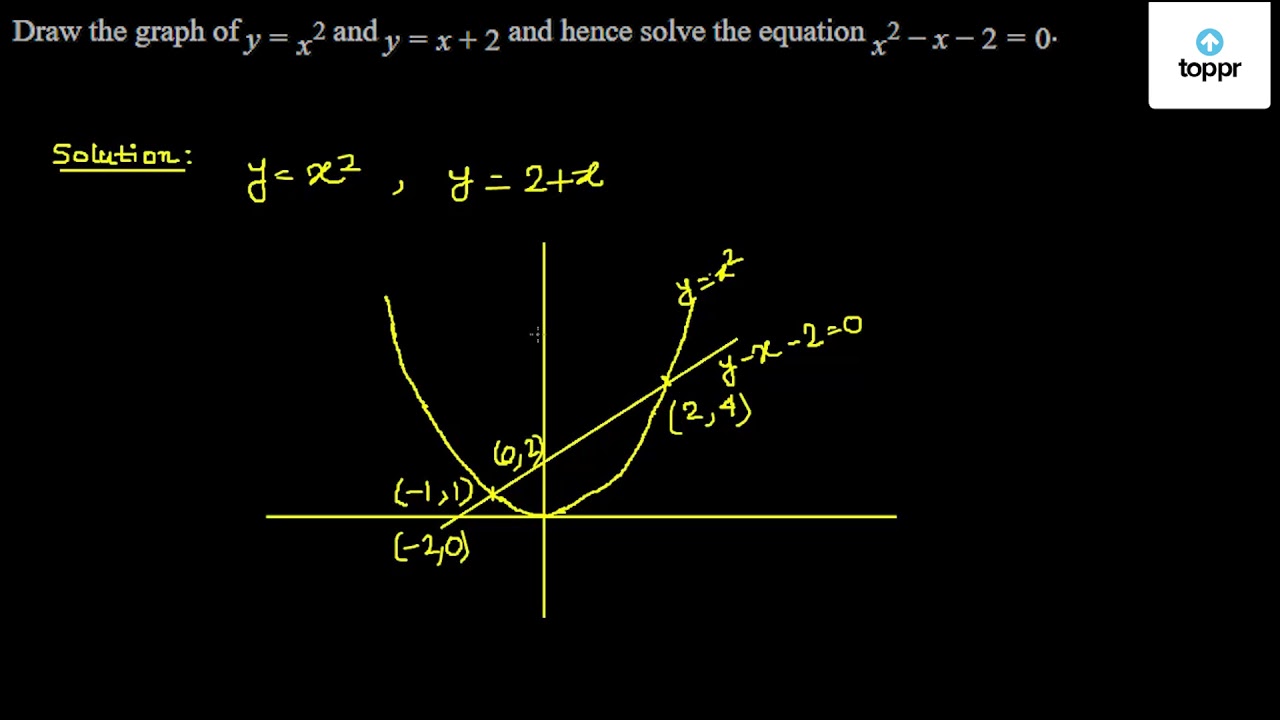
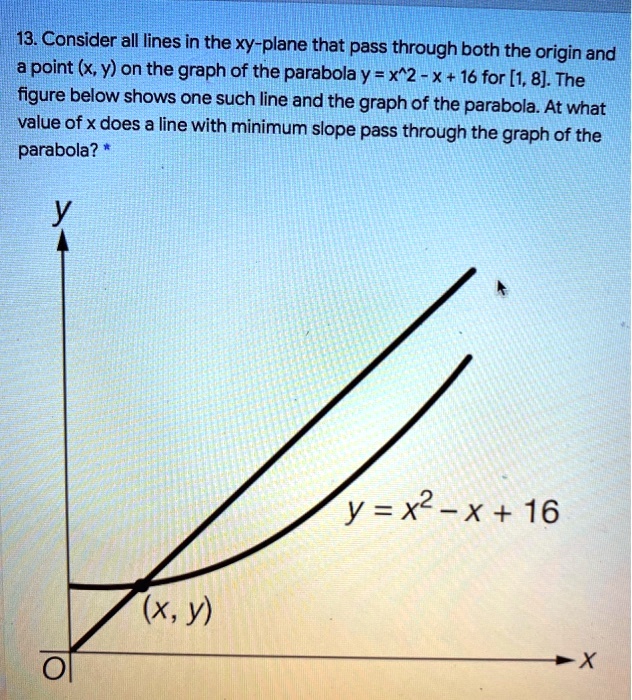
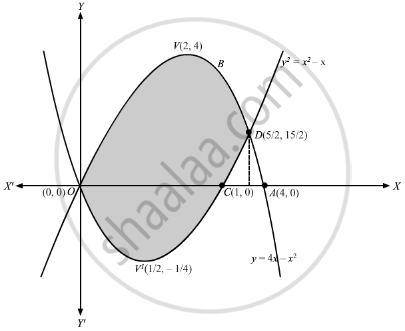
y = √ x (the top half of the parabola);For points of intersection of the equations y=x 2 and y=x ∴x 2−x=0⇒x(x−1)=0 x=0 or x=1⇒Y=0 or y=1 Hence, the coordinates of their points of intersection are O (0, 0) and P (1, 1) ∴ Required area (shaded region) =∫01 (x−x 2)dx= 2x 2 `x^2 = 4py` We can see that the parabola passes through the point `(6, 2)` Substituting, we have `(6)^2 = 4p(2)` So `p = 36/8 = 45` So we need to place the receiver 45 metres from the vertex, along the axis of symmetry of the parabola The equation of the parabola is `x^2 = 18y ` That is `y = x^2 /18`
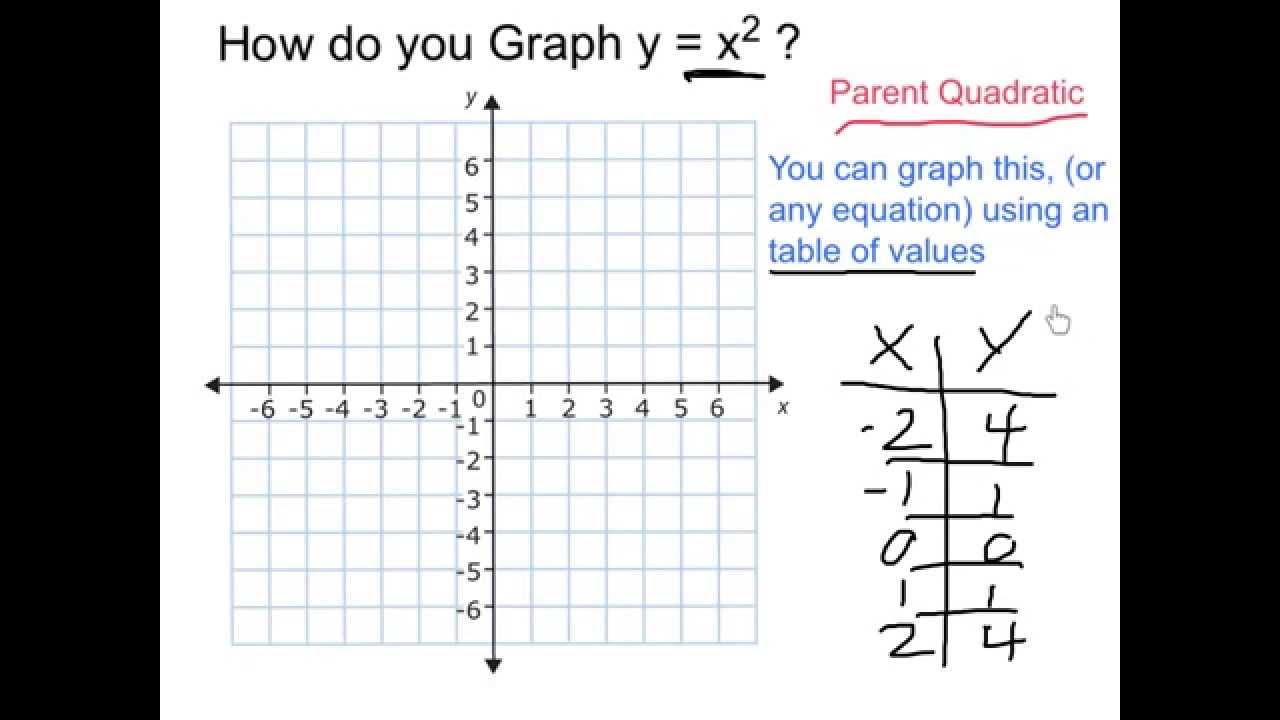
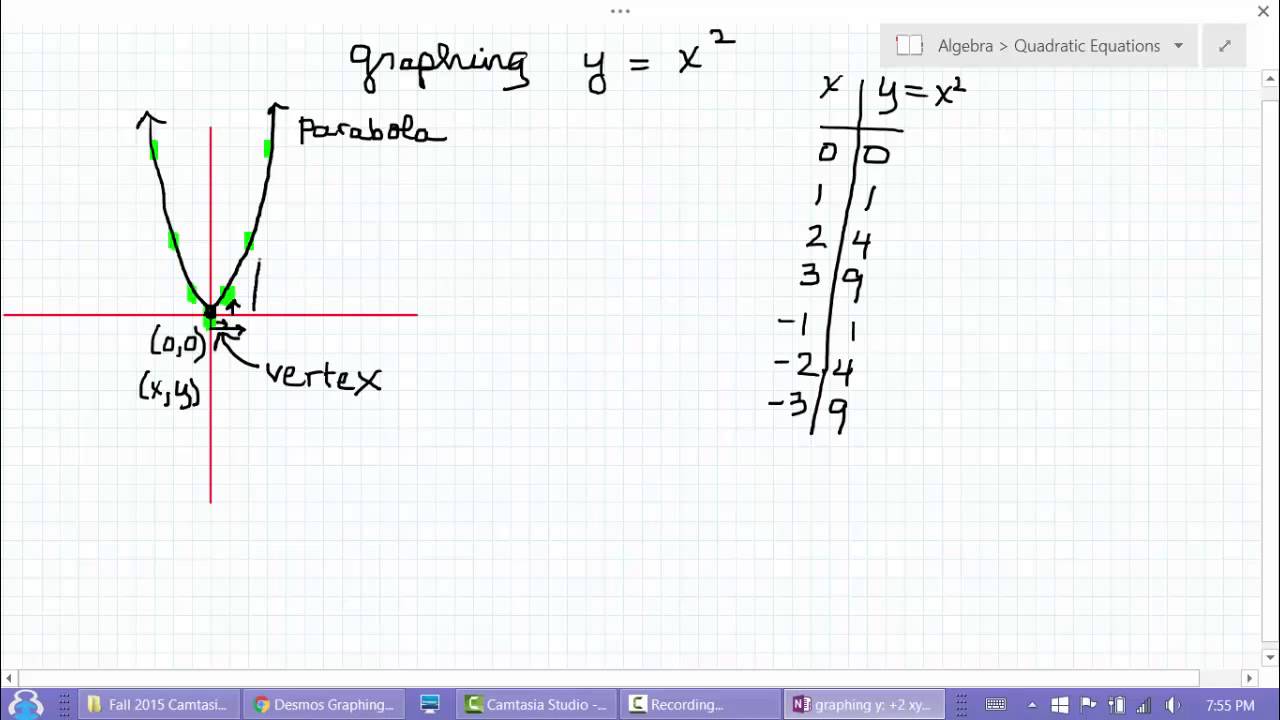
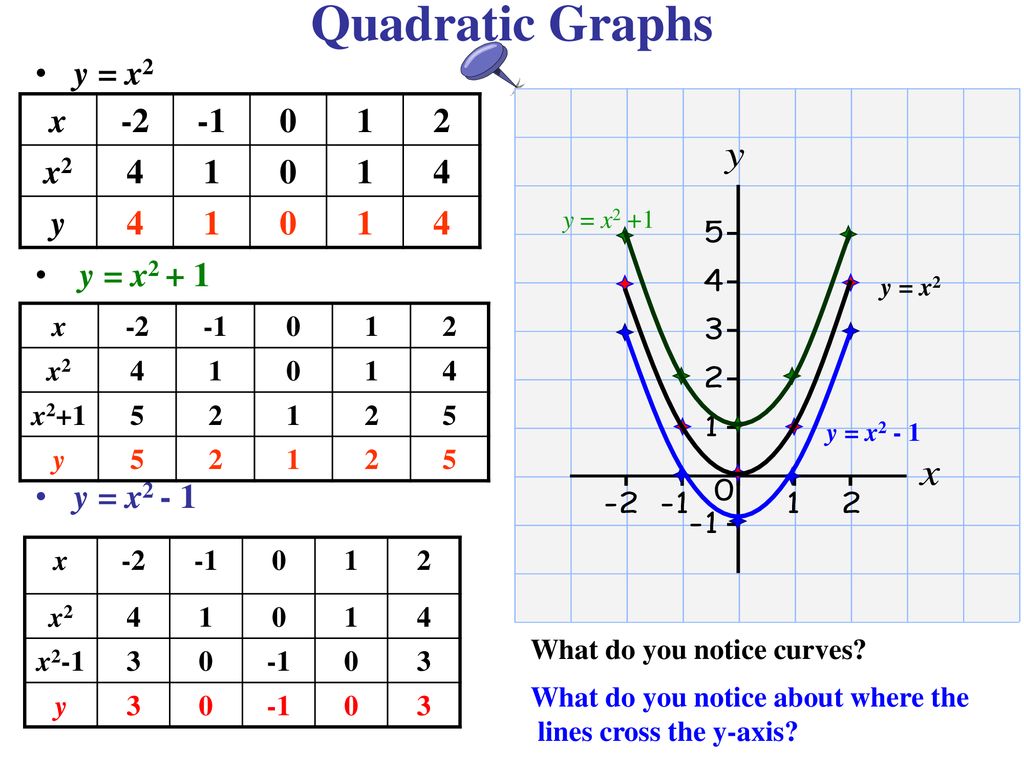
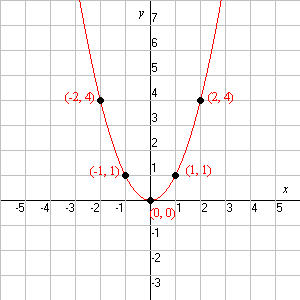
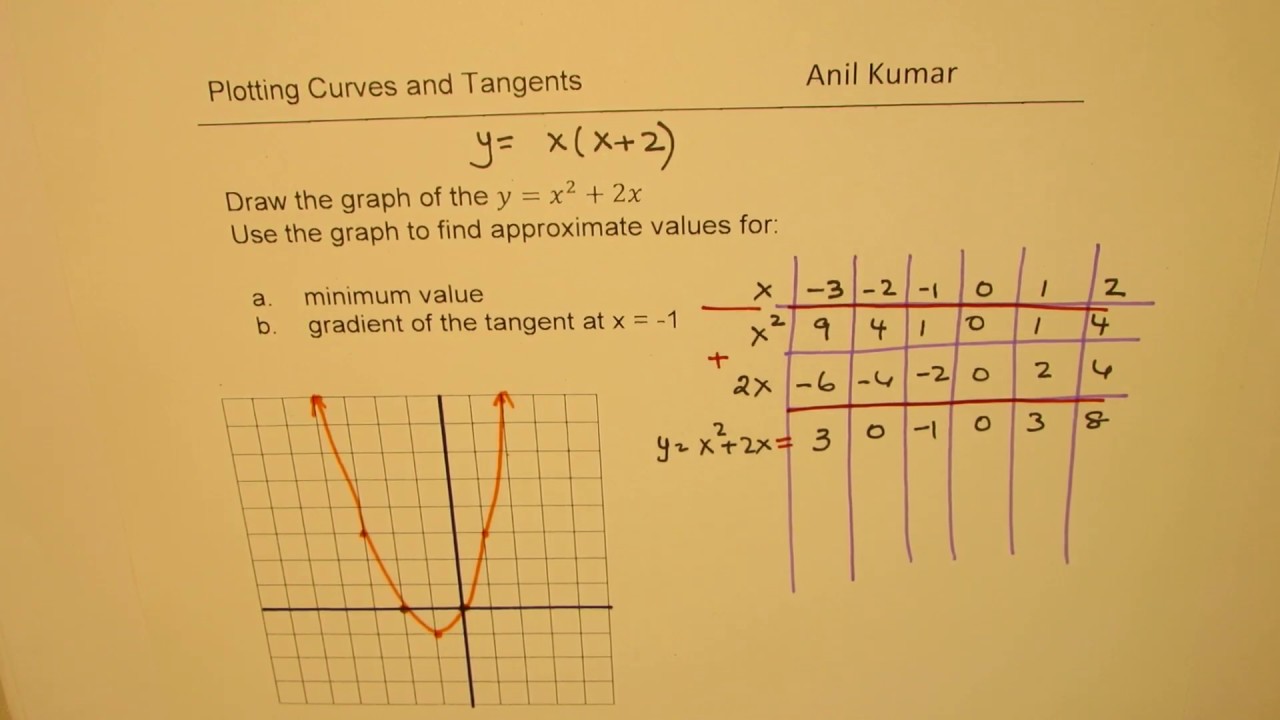
You can put this solution on YOUR website!Answer (1 of 4) Y=05x^2, y=2/3x^2 y=ax^2 is wider than y=x^2 if a is any real number greater than 0 but less than 1 if a is greater than 1 then it will be narrowed IfI do not know how to graph the parabola y= x^2 Plot a few points and draw a smooth curve thru them If x = 2, y = 4 giving you (2,4) If x = 1, y = 1 giving you (1,1) If x = 0, y = 0 giving you (0,0) If x = 1, y = 1 giving you (1,1)
Y=(x-3)^2 parabolaのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 | ||
 |  | |
「Y=(x-3)^2 parabola」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「Y=(x-3)^2 parabola」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「Y=(x-3)^2 parabola」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「Y=(x-3)^2 parabola」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「Y=(x-3)^2 parabola」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「Y=(x-3)^2 parabola」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「Y=(x-3)^2 parabola」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | 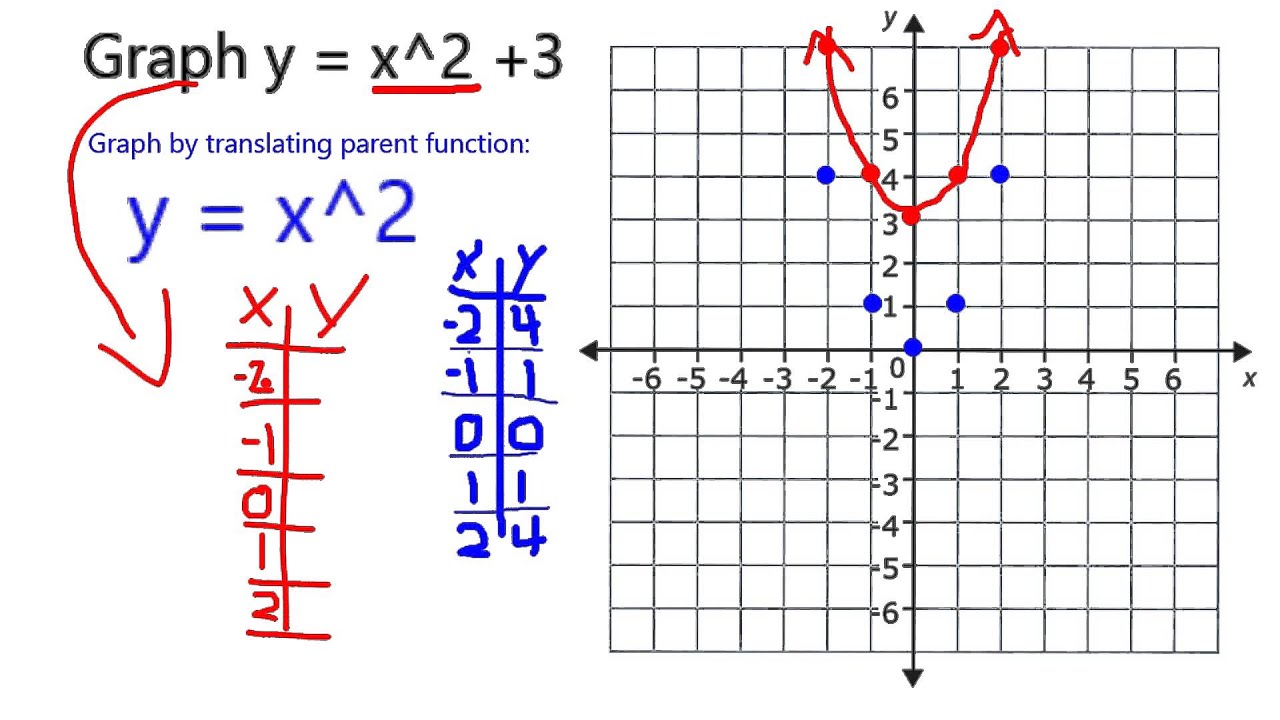 |
「Y=(x-3)^2 parabola」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
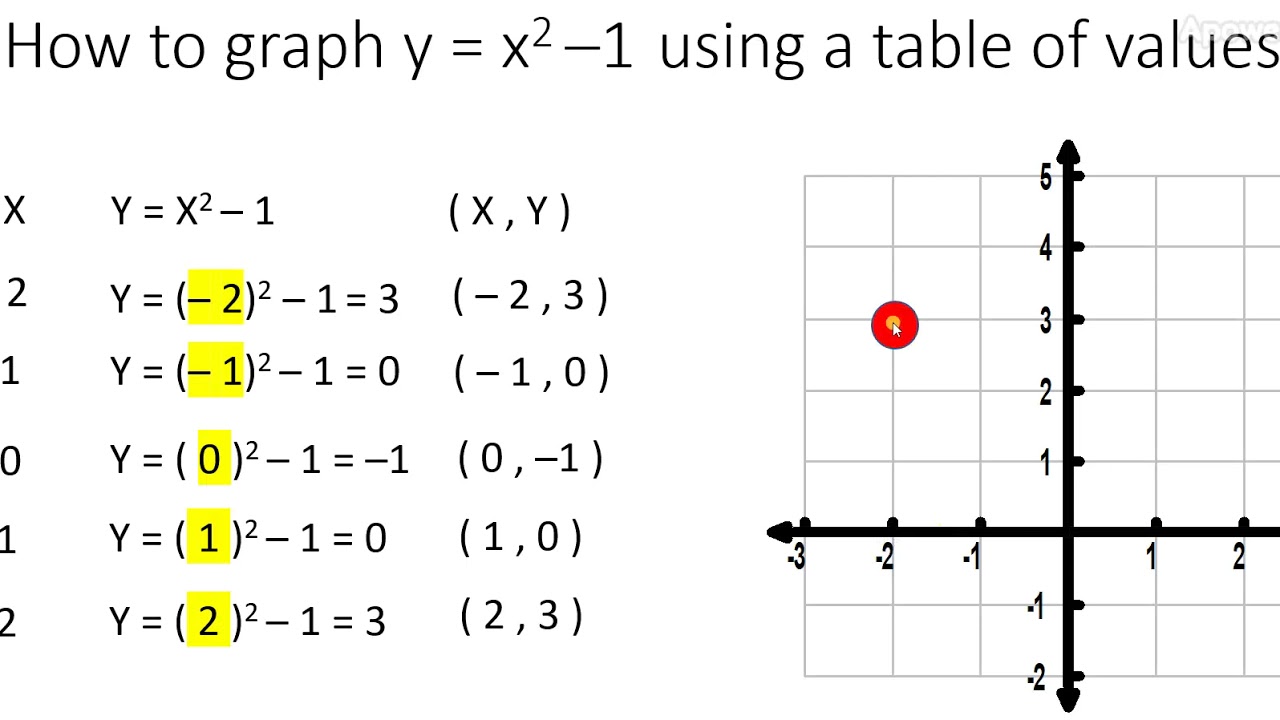 | 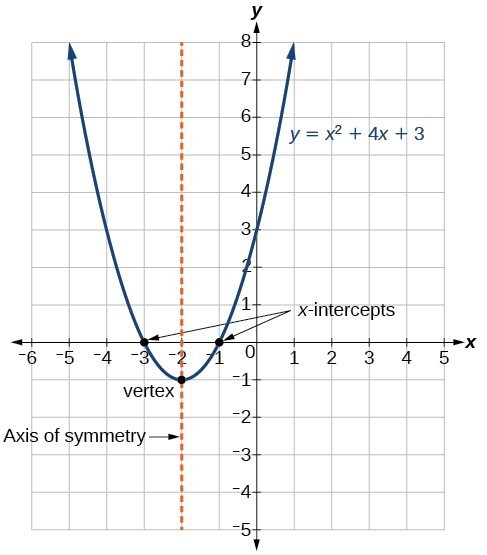 | |
 | 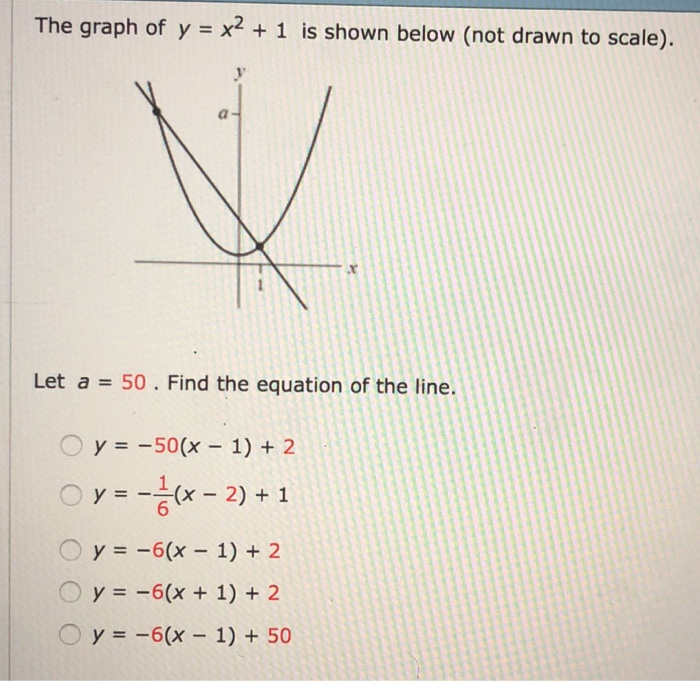 |  |
「Y=(x-3)^2 parabola」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「Y=(x-3)^2 parabola」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「Y=(x-3)^2 parabola」の画像ギャラリー、詳細は各画像をクリックしてください。
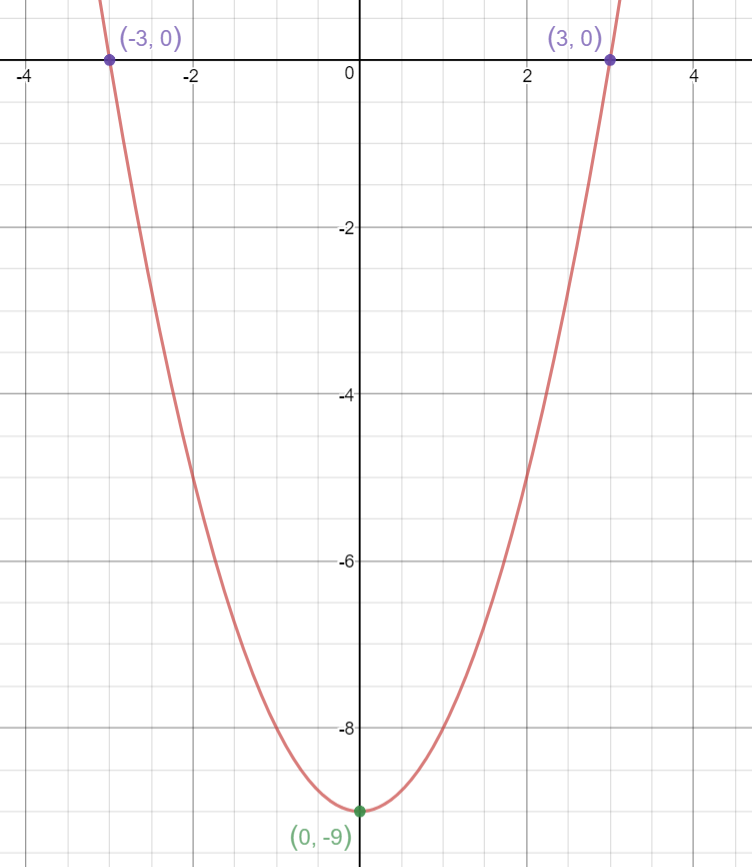 |  | |
 |  |
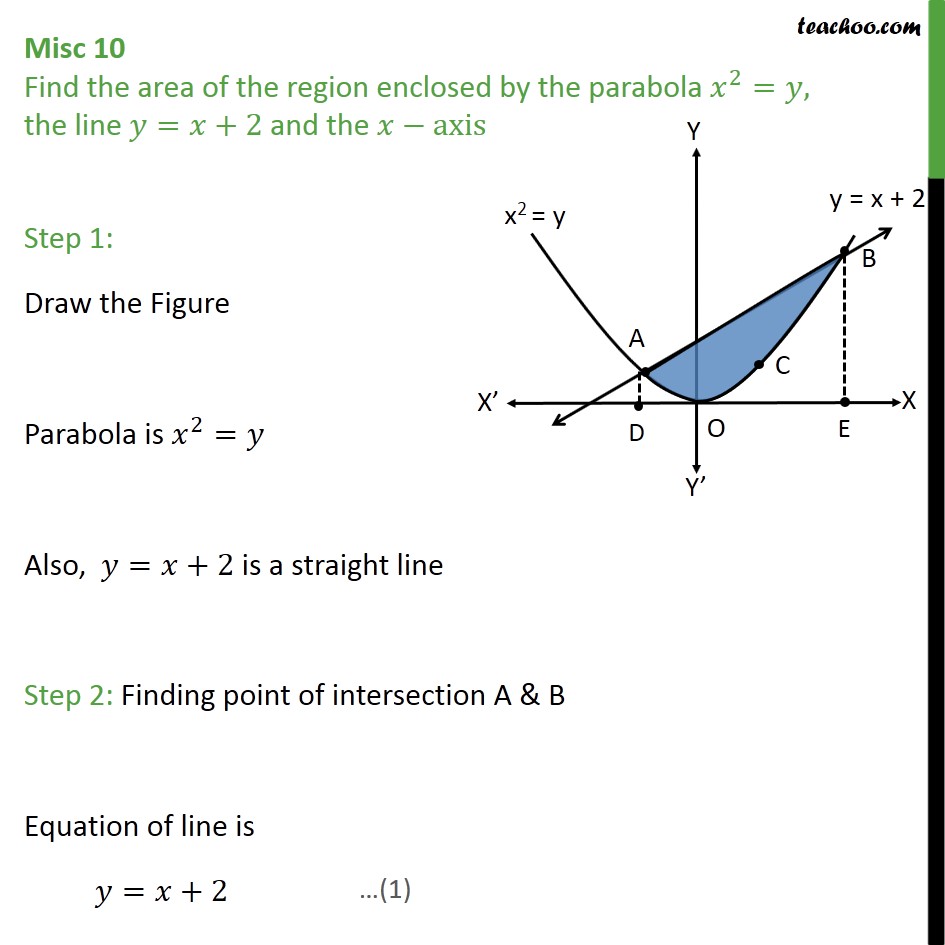
Axis\(y3)^2=8(x5) directrix\(x3)^2=(y1) parabolaequationcalculator en Related Symbolab blog posts Find the area of the region bounded by the parabola $y = 2x^2$, the tangent line to this parabola at $(3, 18)$, and the $x$axis
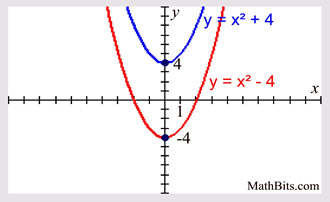
Incoming Term: y=x^2 parabola, y=x^2 graph, y=x^2-1 parabola, y=(x-3)^2 parabola, y=x^2-2x-8 parabola, y=x^2+1 graph, y=f(x-2) graph, y=2x-x^2 graph, y^3=x^2 graph, y=x^2-4 graph,




0 件のコメント:
コメントを投稿